Lezione 6: Complementare di un insieme
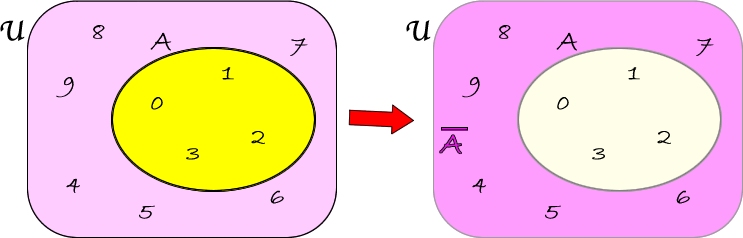
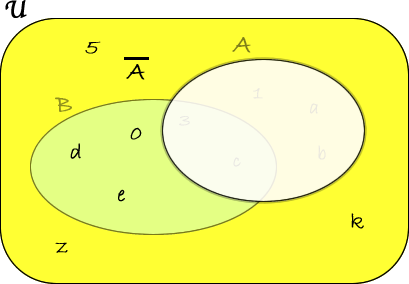
Consideriamo, ora, un insieme\(A\) incluso nell'insieme universo \( \mathfrak{U} \).
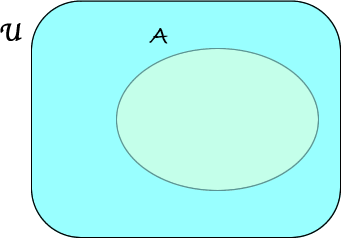
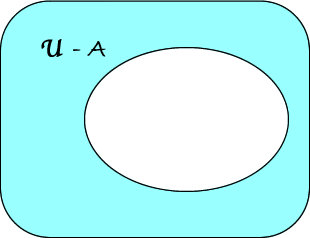
Si chiama complementare di \(A\) e si indica con\( \overline{A} \) la differenza fra insiemi \( \mathfrak{U}-A \):
ESEMPI1) Siano dati \( \mathfrak{U}= \lbrace x: x \) è una cifra (rappresentazione caratteristica) e \(A=\lbrace 0,1,2,3 \rbrace\) Allora \( \overline{A}= \lbrace 4,5,6,7,8,9 \rbrace \).
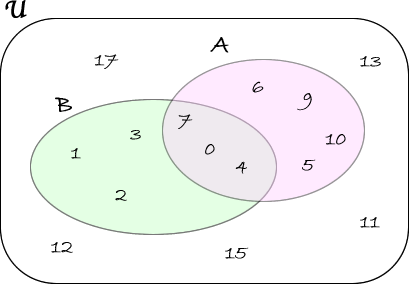
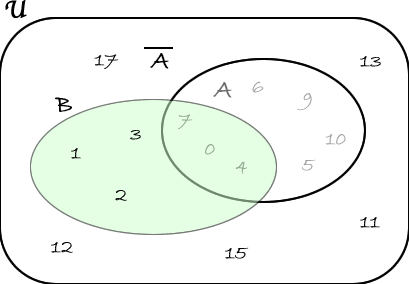
2) Siano dati \( \mathfrak{U}= \lbrace{0,1,2,3,4,5,6,9,10,11,12,13,15,17}\rbrace \), \(A=\lbrace 0,4,5,6,7,9,10\rbrace\) e \(B=\lbrace 0,1,2,3,4,7\rbrace\).
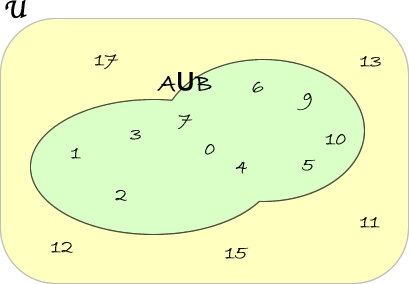
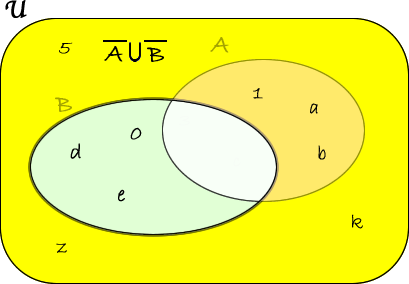
Calcoliamo \( \overline{A\cup B} \). A tal proposito, calcoliamo prima l'unione tra \(A\) e \(B\): \(A \cup B =\lbrace 0,1,2,3,4,5,6,7,9,10\rbrace\).
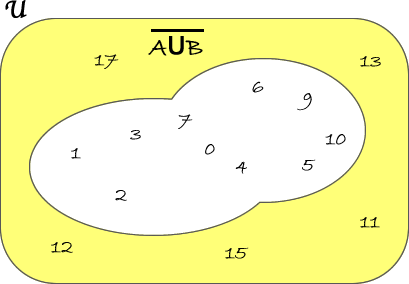
Quindi \( \overline{A\cup B}= \lbrace 11,12,13,15,17 \rbrace \)
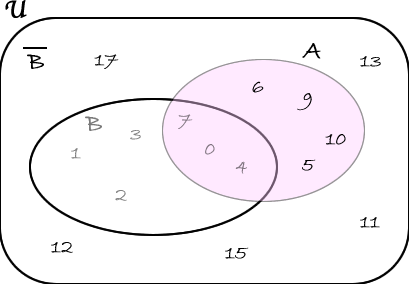
3) Consideriamo gli stessi insiemi dell'esempio precedente. Ossia: \( \mathfrak{U}= \lbrace 0,1,2,3,4,5,6,9,10,11,12,13,15,17 \rbrace \), \(A=\lbrace 0,4,5,6,7,9,10 \rbrace \) e \(B=\lbrace 0,1,2,3,4,7 \rbrace\).
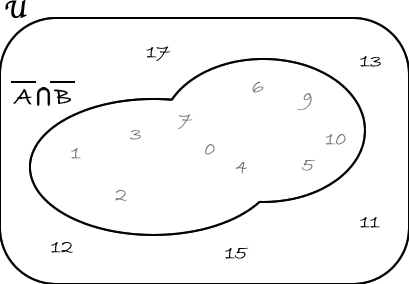
Calcoliamo, ora, \( \overline{A}\cap \overline{B} \): \( \overline{A}= \lbrace{1,2,3,11,12,13,15,17}\rbrace \) e \( \overline{B}= \lbrace{5,6,9,10,11,12,13,15,17}\rbrace \) Quindi
Pertanto: \( \overline{A}\cap \overline{B} = \lbrace 11,12,13,15,17 \rbrace\).
|
Gli esempi 2) e 3) evidenziano una legge che è sempre valida:
Prima legge di De Morgan:
\( \overline{A \cup B} = \overline{A} \cap \overline{B} \)
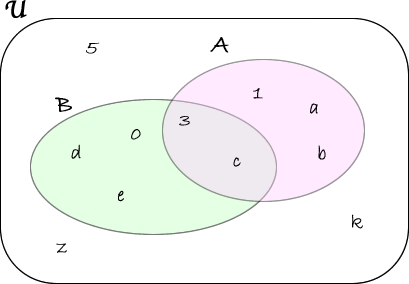
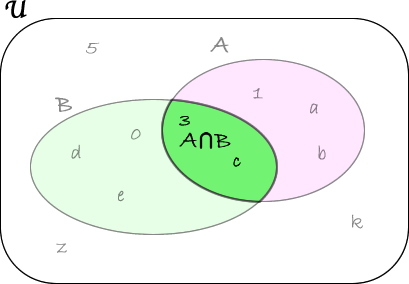
ESEMPI4) Siano dati \( \mathfrak{U}= \lbrace 0,1,3,5,a,b,c,d,e,k,z \rbrace \), \(A=\lbrace 1,3,a,b,c \rbrace\) e \(B=\lbrace 0,3,c,d,e \rbrace\).
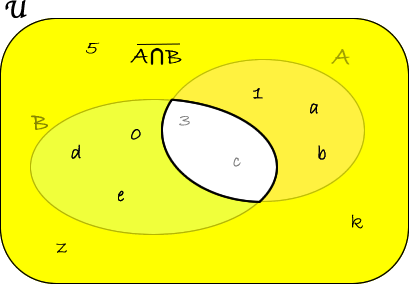
Calcoliamo \( \overline{A \cap B} \). A tal proposito, calcoliamo prima l'intersezione tra \(A\) e \(B\): \( A\cap B =\lbrace 3,c\rbrace\).
Quindi \( \overline{A \cap B}=\lbrace 0,e,d,1,a,b,5,z,k \).
5) Consideriamo gli stessi insiemi dell'esempio precedente. Ossia: \( \mathfrak{U}= \lbrace 0,1,3,5,a,b,c,d,e,k,z \rbrace \), \(A=\lbrace 1,3,a,b,c \rbrace\) e \(B=\lbrace 0,3,c,d,e \rbrace\).
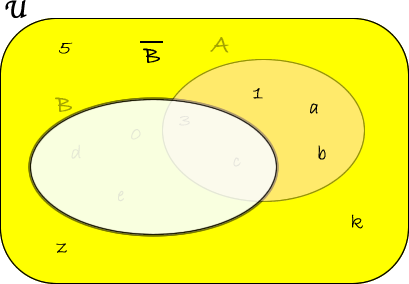
Calcoliamo, ora, \(\overline {A} \cup \overline{B}\). \(\overline{A}=\lbrace 5,0,d,e,z,k\rbrace\) e \(\overline{B}=\lbrace 5,1,a,b,z,k\rbrace\) Quindi:
Pertanto: \(\overline{A} \cup \overline{B}=\lbrace 5,1,0,a,b,d,e,k,z\rbrace\)
|
Gli esempi 4) e 5) evidenziano un'altra legge, anch'essa sempre valida:
Seconda legge di De Morgan:
\( \overline{A \cap B} = \overline{A} \cup \overline{B} \).