Dati due insiemi \( A \) e \( B \) chiamiamo intersezione di \( A \) e \( B \), e indicheremo con \( A \cap B \) l'insieme degli elementi che appartengono ad entrambi gli insiemi.



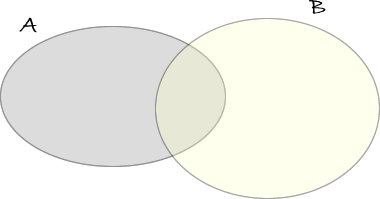
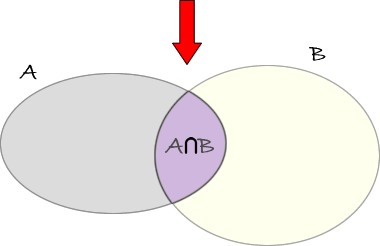
ESEMPI

1) Supponiamo di avere i due insiemi (rappresentazione tabulare) \( A= \lbrace{1,4,6,10,12}\rbrace \) e \( B= \lbrace{1,3,5,6,13}\rbrace \)

Allora \( A \cap B = \lbrace{1,6}\rbrace \).


2) Siano dati i due insiemi (rappresentazione caratteristica) 

\( A= \lbrace x: x \) è un numero multiplo di 4 minore di 40\(\rbrace\) e 

\( B= \lbrace x: x \) è un numero multiplo di 5 minore di 50\(\rbrace\).

Nella rappresentazione tabulare avremo \( A= \lbrace{4,8,12,16,20,24,28,32,36}\rbrace \) e \( B= \lbrace{5,10,15,20,25,30,35,40,45}\rbrace \).

Allora \( A\cap B= \lbrace{20}\rbrace \).


3) Supponiamo di avere gli insiemi (rappresentazione tabulare) \( A= \lbrace{1,3,5,7,9,11}\rbrace \) e \( B= \lbrace{0,2,4,6,8,10,12}\rbrace \).



In questo caso i due insiemi non hanno alcun elemento in comune, quindi scriveremo \( A\cap B= \emptyset\).


Nei casi simili a quest'ultimo esempio 3), ossia con intersezione uguale all'insieme vuoto, i due insiemi si dicono disgiunti.

Last modified: Tuesday, 22 August 2017, 4:04 PM