Lezione 2: i Sottoinsiemi

Un insieme che non contiene elementi si chiama insieme vuoto e si indica utilizzando il simbolo 

\( \emptyset \).

Dati due insiemi  A e B , supponiamo che il secondo sia contenuto nel primo, ossia che ogni elemento del secondo sia anche elemento del primo, e che ci sia qualche elemento del primo non appartenente al secondo.

Utilizzando i diagrammi di Eulero-Venn, supponiamo quindi che la situazione sia la seguente.

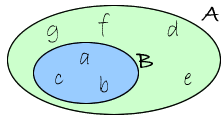
In tali casi diciamo che B è un sottoinsieme proprio di A e scriveremo:

\( B \subset A \)          (B è strettamente contenuto, incluso in A) 

oppure 

\( A \supset B \)           (A strettamente contiene, include B).

Quando incontreremo, invece, una scrittura come la seguente:

\( B \subseteq A \)          (B è contenuto, incluso in A) 

oppure 

\( A \supseteq B \)          (A contiene, include B), 

supporremo che ogni elemento di B appartenga ad A, includendo anche il caso in cui A e B contengano gli stessi elementi.

Se, poi, gli elementi di A appartengono anche a B e, viceversa, gli elementi di B appartengono ad A, diremo che A e B sono uguali e scriveremo:

\( A=B \)

Quando ciò non avviene si scrive anche:

\( A \neq B \).